Let’s make 1/f noise easily! Methodology and Theoretical Background

Toon Robotics is supported by its audience. When you purchase through links on my site, I may earn an affiliate commision.
Introduction
This article explains the easy generation of 1/f noise, also called 1/f fluctuation. It shows how to create natural movements and pleasant rhythms using a program. It also discusses the theoretical background of the method using intermittent chaos.
In summary
The intermittent chaos method can create 1/f noise easily. The formulas below represent the B=2 one-dimensional modified Bernoulli map, which generates intermittent chaos. This map is a 1/f fluctuation, so the method is often referred to as the intermittent chaos method.
$$x_{n+1}=\begin{cases}
x_n + 2x_n^2 & (0 \leq x_n \leq 0.5) \\
x_n – 2(1-x_n)^2 & (0.5 < x_n \leq 1)
\end{cases}$$
The beginning of the matter
I wanted to use 1/f noise for a robot. I found websites that explained how to generate it. Most of them used the “intermittent chaos method.” This method creates fluctuation in LED candles and only needs simple calculations.
Many websites presented intermittent chaos methods implemented using formulas, such as the following.
$$x_{n+1}=\begin{cases}
x_n + 2x_n^2 & (0 \leq x_n \leq 0.5) \\
x_n – 2(1-x_n)^2 & (0.5 < x_n \leq 1)
\end{cases}$$
The websites provided vague information. They either quoted from other websites or had no theoretical background. The content was just vague, like saying, “I heard this can be done.”
Therefore, in this article, I will delve deeper into this “intermittent chaos method,” including what it is and what logic is used to achieve 1/f fluctuation.
What is 1/f fluctuation?
A 1/f fluctuation was found when measuring the noise of electron flow in a vacuum tube [Musha, 1991]. It is a signal or motion where the power of change in a time-series signal is proportional to the inverse of its frequency [Aihara, 1995].
It is sometimes called pink noise [Musha, 1980].
We commonly observe 1/f fluctuation in various natural phenomena and human physiological signals. It can be observed in automobile flow, cosmic rays, wood grain patterns, heartbeats, and body swaying when standing upright [Aihara, 1995][Musha, 1980].
This may sound difficult to write, but it is an irregular but slightly regular movement that is often seen in nature.
Because of this property, 1/f fluctuation is used to make LED lights flicker like a real candle flame, and is also used to blow air from an electric fan.
How to create 1/f fluctuation and intermittent chaos
Unlike observing movement in nature, we have to create 1/f fluctuation intentionally to use.
There are various methods available to create 1/f fluctuation.
- Method using thermal noise of resistor [Doi, 1997]
- Methods using intermittent chaos.
- Method of 1/2-order integration of white noise [Tanaka, 1996].
- FFT→1/f filter→IFFT of a signal [Doi, 1997].
The “method using intermittent chaos” is commonly used because it is simple and requires less computation.
Aihara describes intermittent chaos as follows[Aihara, 1995].
Chaos such that steady state and irregular signals occur intermittently.
(The references cited are in Japanese.)
Disregarding the strict definition, signals appear and disappear in non-periodic, irregular patterns and constant states.
A simple one-dimensional mapping can generate intermittent chaos.
One of them is called the one-dimensional modified Bernoulli map.
The following expresses the one-dimensional modified Bernoulli map [Aizawa, 1984][Aizawa, 1989].
$$x_{n+1}=\begin{cases}
x_n + 2^{B-1}x_n^B & (0 \leq x_n \leq 0.5) \\
x_n – 2^{B-1}(1-x_n)^B & (0.5 < x_n \leq 1)
\end{cases}$$
This one-dimensional modified Bernoulli map yields 1/f fluctuations when B=2 [Yamada, 2013].
The case B=2 means that
$$x_{n+1}=\begin{cases}
x_n + 2x_n^2 & (0 \leq x_n \leq 0.5) \\
x_n – 2(1-x_n)^2 & (0.5 < x_n \leq 1)
\end{cases}$$
which is the very formula introduced as the intermittent chaos method.
Below, I summarize the process.
- Intermittent chaos from one-dimensional mapping may generate 1/f fluctuation.
- One known example is the case B=2 of a one-dimensional modified Bernoulli map.
- One-dimensional modified Bernoulli maps are prevalent because of their simple computation.
The method was thus named the Intermittent Chaos Method because of its use of intermittent chaos.
Let’s experiment.
Let’s analyze this in a Python environment using NumPy’s fft.
I try to generate 1/f fluctuation with the following function.
def fluctuation_1_f(x):
if x <= 0.05 or x >= 0.95:
return random.random()
if x < 0.5:
return x + 2 * x * x
elif x < 0.95:
return x - 2.0 * (1.0 - x) * (1.0 - x)It implements the formula for the one-dimensional modified Bernoulli map described earlier. Figure 1 shows this generated data.
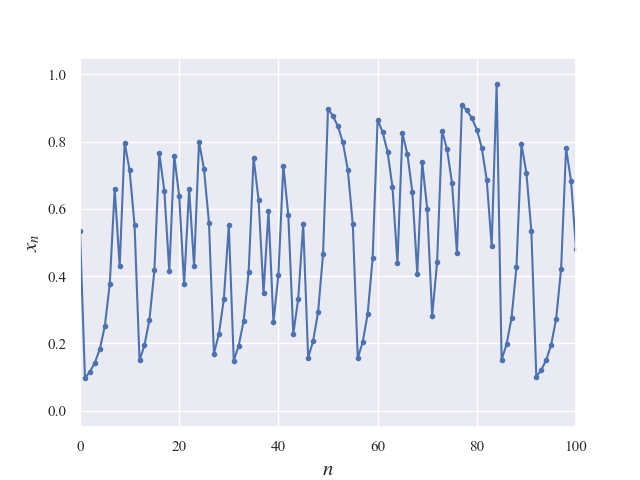
The movement seems random, but it occasionally stays at a specific point for a while. The value range is [0,1]. If the value is too close to 0 or 1, it stays for too long. Figure 2 shows this. To fix this, we randomly reset the value if it is below 0.05 or above 0.95.
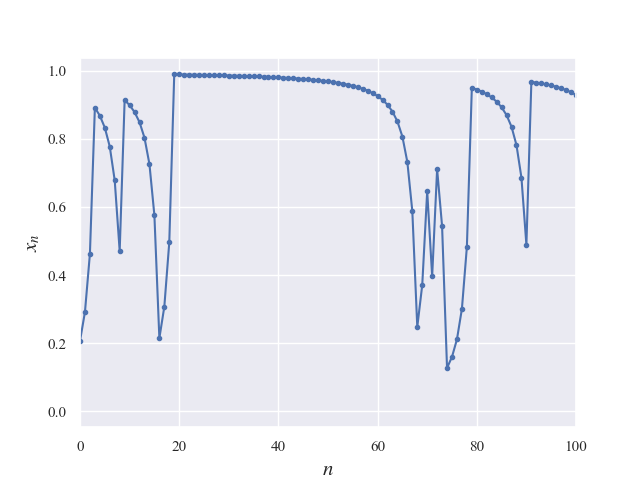
Let’s analyze the behavior shown in the graph in Figure 1. We can perform a Fourier transform to examine the relationship between frequency and power spectrum, as shown in Figure 3.
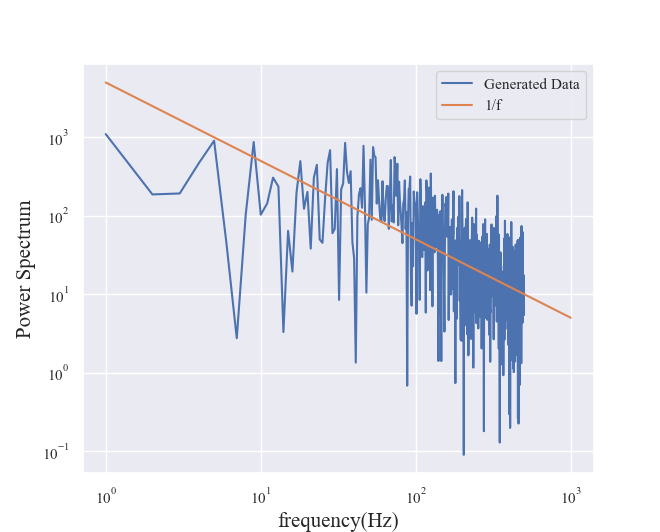
The blue line is the generated data, and the orange line is the slope -1 on both logarithmic graphs, i.e., the straight line when the frequency is 1/f relative to f. You can see that the generated data roughly follows the slope -1.
We can now confirm the successful generation of 1/f fluctuations.
For the latest status, check here.
References
[Musha, 1991] 武者利光, 沢田康次, ゆらぎ・カオス・フラクタル, 日本評論社, 1991. (in Japanese)
[Aihara, 1995] 合原一幸, 五百旗頭正編著, カオス応用システム, 朝倉書店, 1995. (in Japanese)
[Musha, 1980] 武者利光, ゆらぎの世界, 講談社, 1980. (in Japanese)
[Doi, 1997] 土井滋貴, 大塚智仁, 高橋晴雄, 照明における1/fゆらぎ制御法の実験的検討, 電気学会論文誌C, Vol. 117, No.4, pp.409-415, 1997. (in Japanese)
[Tanaka, 1996] 田中一男編著, インテリジェント制御システム, 共立出版株式会社, 1996. (in Japanese)
[Aizawa, 1984] Y. Aizawa and T. Kohyama, Asymptotically Non-Stationary Chaos, Progress of Theoretical Physics, Vol. 71, No. 4, pp. 847-850, 1984.
[Aizawa, 1989] Y. Aizawa, Y. Kikuchi, T. Harayama, K. Yamamoto, M. Ota and K. Tanaka, Stagnant Motions in Hamiltonian Systems, Progress of Theoretical Physics Supplement, vol. 98, pp. 36–82, 1989.
[Yamada, 2013] 山田光宏, カオス性の異なる1/fゆらぎを用いた拍手のアニメーションの感性評価, 日本感性工学会論文誌, Vol.12, No. 3, pp.389-396, 2013. (in Japanese)
