1/fゆらぎを作ろう!手法と理論的背景の徹底解説!

はじめに
今回は自然な動作や心地よいリズムを作り出すための1/fゆらぎを簡単に発生させる方法についてプログラム付きで解説します。更にその手法である間欠性カオスを使った方法とは何なのか、理論的背景についても深堀りしていきます。
まとめると…
1/fゆらぎは間欠性カオスを用いた方法で簡単に作ることができる。その式は
$$x_{n+1}=\begin{cases}
x_n + 2x_n^2 & (0 \leq x_n \leq 0.5) \\
x_n – 2(1-x_n)^2 & (0.5 < x_n \leq 1)
\end{cases}$$
で表すことができる。
この数式は間欠性カオスを発生させる1次元変形ベルヌーイ写像の\(B=2\)の場合であり、この写像は1/fゆらぎとなることが知られている。こうした理由から、上記の方法は間欠カオス法として紹介されている。
ことの発端
ロボットの動作に利用するため、1/fゆらぎを利用しようと考えたときのこと。インターネット上で1/fゆらぎを発生させる方法について調べると、いくつか解説しているサイトを発見しました。その多くはLEDキャンドルのゆらぎに利用しているもので、非常に簡潔な計算で実現可能な「間欠カオス法」というものでした。
間欠カオス法として紹介されているものはだいたい以下のような数式に基づいて実装されていました。
$$x_{n+1}=\begin{cases}
x_n + 2x_n^2 & (0 \leq x_n \leq 0.5) \\
x_n – 2(1-x_n)^2 & (0.5 < x_n \leq 1)
\end{cases}$$
一方でそれらサイトもどこか別のサイトからの引用であったり、理論的なバックグラウンドが示されておらず、「これでできるらしいよ…」という不明瞭な内容であったり、非常に曖昧な情報に終始していました。
そこでこの記事ではこの「間欠カオス法」とは何なのか、どういう理屈で1/fゆらぎが実現されているのか、というところも含めて深堀りしていきます。
そもそも1/fゆらぎとは
1/fゆらぎとは真空管の中を流れる電子流の雑音を測っていて見つかったもので[武者, 1991]
時系列信号の変化のパワーが周波数の逆数に比例する信号や動き
のことを指します[合原, 1995] 。
ピンク雑音と呼ばれることもあります[武者, 1980]。
この1/fゆらぎは自然現象や人体の生理信号などで広く観測され、自動車の流れ、宇宙線、木目の模様、心拍や直立時の身体の揺れなどに現れます[合原, 1995][武者, 1980]。
こう書くと何やら難しそうですが、要は
自然界でよく見られる、不規則だけど、少しだけ規則性のある動き
のことです。
こうした性質から、1/fゆらぎはLEDライトを本物のロウソクの炎のように揺らがせたり、扇風機の送風に応用したりといった利用がされています。
1/fゆらぎの作り方と間欠性カオス
自然界の何らかの動きを観測する場合と違って、実際にこの1/fゆらぎを用いるためには、1/fゆらぎ自体を人工的に作り出す必要があります。
1/fゆらぎを作り出す手法には以下のような複数の手法があるようです。
- 抵抗の熱雑音を利用する方法[土井, 1997]
- 間欠性カオスを用いた方法
- 白色ゆらぎを1/2階積分する方法[田中, 1996]
- 信号をFFT→1/fフィルタ→IFFTする方法[土井, 1997]
この内、実装が簡単で計算量も少なくて済む「間欠性カオスを利用した方法」がよく用いられています。
間欠性カオス(Intermittent Chaos)は以下のように説明されています[合原, 1995]。
定常状態と不規則な信号が間欠的に発生するようなカオスのこと
厳密な定義は置いておいて、要は周期的じゃない不規則な状態と値が変化しない状態が起きたりやんだりする信号ということですね。
こうした間欠性カオスは簡単な1次元写像によって発生させることが可能であることが知られています。
その中の一つが1次元変形ベルヌーイ写像と呼ばれるものです。
1次元変形ベルヌーイ写像は次のように表されます[Aizawa, 1984][Aizawa, 1989]。
$$x_{n+1}=\begin{cases}
x_n + 2^{B-1}x_n^B & (0 \leq x_n \leq 0.5) \\
x_n – 2^{B-1}(1-x_n)^B & (0.5 < x_n \leq 1)
\end{cases}$$
この1次元変形ベルヌーイ写像は\(B=2\)の場合に1/fゆらぎが得られることが知られています[山田, 2013]。
\(B=2\)の場合とはすなわち
$$x_{n+1}=\begin{cases}
x_n + 2x_n^2 & (0 \leq x_n \leq 0.5) \\
x_n – 2(1-x_n)^2 & (0.5 < x_n \leq 1)
\end{cases}$$
となり、間欠カオス法として紹介されていた数式そのものとなります。
つまり流れをまとめると
- 1次元写像によって発生する間欠性カオスにおいて、1/fゆらぎが得られるものがある。
- その一つの例として、1次元変形ベルヌーイ写像のB=2の場合が知られている。
- 1次元変形ベルヌーイ写像は簡単に計算可能であるため、広く利用されている。
ということで、間欠性カオスを利用した手法であることから間欠カオス法(間欠性カオス法といったほうが正確な気がします)という名前で紹介されていた、というわけです。
実験してみよう
実際にPython環境で試してみましょう。numpyのfftを使って分析していきます。
次のような関数を使って1/fゆらぎを発生させてみます。
def fluctuation_1_f(x):
if x <= 0.05 or x >= 0.95:
return random.random()
if x < 0.5:
return x + 2 * x * x
elif x < 0.95:
return x - 2.0 * (1.0 - x) * (1.0 - x)先述の1次元変形ベルヌーイ写像の式を実装しています。これで生成したデータは次のようになりました。(図1)
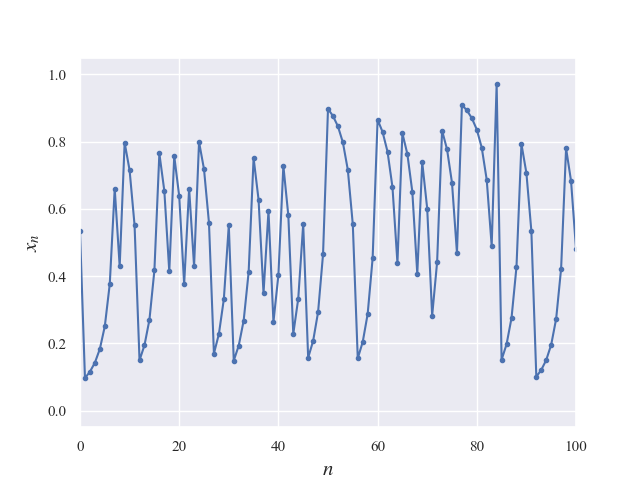
おおよそランダムな動きに見えますが、時折特定の点に長く滞留しているような挙動が見えますね。ちなみに値域は[0,1]となりますが、0か1に近すぎると図2のように滞留しすぎてしまうため0.05以下及び0.95以上でランダムに値を取り直す処理を入れています。
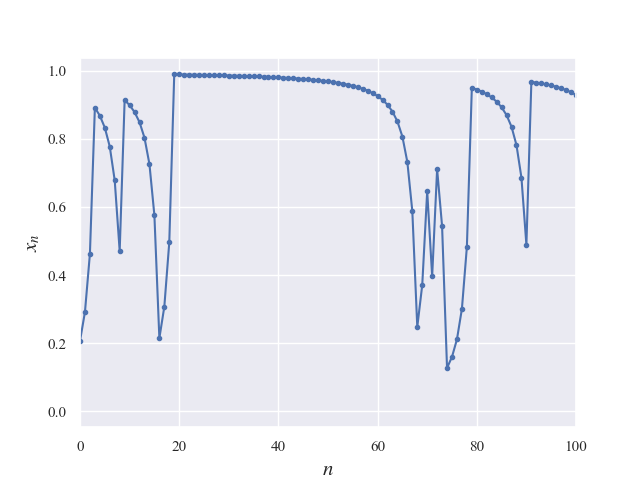
図1のグラフで示した挙動を分析してみます。フーリエ変換を行い、周波数とパワースペクトルの関係を見てみます(図3)。
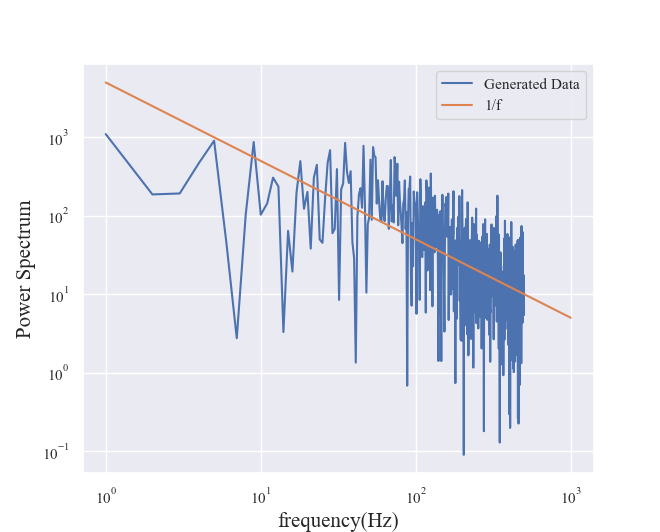
青線が生成データ、オレンジの線が両対数グラフにおける傾き-1、つまり周波数fに対し1/fとなる場合の直線です。生成データがおおよそ傾き-1に従っていることがわかりますね。
これで無事1/fゆらぎが生成できていることが確認できました。
最新情報はこちら!
最新の開発状況は以下で公開中です!ぜひご覧ください!
参考文献
[武者, 1991] 武者利光, 沢田康次, ゆらぎ・カオス・フラクタル, 日本評論社, 1991.
[合原, 1995] 合原一幸, 五百旗頭正編著, カオス応用システム, 朝倉書店, 1995.
[武者, 1980] 武者利光, ゆらぎの世界, 講談社, 1980.
[土井, 1997] 土井滋貴, 大塚智仁, 高橋晴雄, 照明における1/fゆらぎ制御法の実験的検討, 電気学会論文誌C, Vol. 117, No.4, pp.409-415, 1997.
[田中, 1996] 田中一男編著, インテリジェント制御システム, 共立出版株式会社, 1996.
[Aizawa, 1984] Y. Aizawa and T. Kohyama, Asymptotically Non-Stationary Chaos, Progress of Theoretical Physics, Vol. 71, No. 4, pp. 847-850, 1984.
[Aizawa, 1989] Y. Aizawa, Y. Kikuchi, T. Harayama, K. Yamamoto, M. Ota and K. Tanaka, Stagnant Motions in Hamiltonian Systems, Progress of Theoretical Physics Supplement, vol. 98, pp. 36–82, 1989.
[山田, 2013] 山田光宏, カオス性の異なる1/fゆらぎを用いた拍手のアニメーションの感性評価, 日本感性工学会論文誌, Vol.12, No. 3, pp.389-396, 2013.
